Ok, yet more Zero Hedge (ZH). (See also: Parts one, two, and three.) Here’s today’s bit:
This can only go on so long as vol arbitrageurs will creep up the moneyness curve (to hedge the tail risk) and eventually impact the ATM. This happened in early 2010 and is happening again currently.
This is the heart-stopping passage that finally induces me to suggest that the author is a nincompoop.
Smoke
These sentences are a perfect example of why it takes so long to wade through this dreck. Look at the number of questions that they raise:
- What’s a “vol arbitrageur”? What does he do?
- What’s the “moneyness curve”?
- What does “hedging the tail risk” mean? Is this relevant to whatever it is that “vol arbitrageurs” do?
- Would such hedging require “creeping up the moneyness curve”?
- Would such creeping eventually affect the at the money options?
- Did this in fact happen in early 2010?
- Is this in fact happening now?
I would point out that it’s much easier to blow this smoke than to see through it. I’m developing the impression that our author is more interested in hand-waving and jargon-spitting in an effort to sound smart than in making a tight or informative argument.
Volatility Arbitrage
A “vol arbitrageur” is presumably someone who engages in volatility arbitrage. Such traders place bets on whether the current implied volatility of an option is too low or too high vs. the eventually realized volatility of the underlying asset. They place these bets by buying and selling portfolios of options paired with their underlying assets. Their goal is to construct a portfolio with a value that is insensitive to the underlying asset’s price, but sensitive to changes in that asset’s realized and expected volatility, which they hope to have predicted more accurately than the market as a whole.
If a volatility arbitrageur is betting that the market is underestimating an asset’s future volatility, he will buy options (either puts or calls; it doesn’t matter), and if he’s betting that the market is overestimating that volatility, he will sell options.
Moneyness
Moneyness is “is a measure of the degree to which a derivative is likely to have positive monetary value at its expiration”. An option with 25% moneyness has a 25% chance of expiring in the money (with a strike price above market price for a put, or below for a call).
Of course, moneyness (as a hard number) is sort of bunk. No one knows the future, or even the probability distribution of the future. It appears that the computation of moneyness assumes that the probability distribution of the underlying asset’s value at expiry is normal; this is precisely the assumption that the market is not making, as measured by the SKEW index.
As a qualitative term, however, moneyness can be taken to mean the “goodness” of an option’s strike price. Low for calls, high for puts.
Hedging
The author makes reference to “hedg[ing] the tail risk”. In general terms, this refers to creating a portfolio that protects one against very unlikely, but very bad (“tail”) outcomes. For instance, if you buy an asset, you might also buy an out of the money put option to protect yourself from catastrophic drops in the asset’s value.
Volatility arbitrageurs do attempt to hedge their positions so that they are only sensitive to changes in volatility, and not asset value. Whether they also attempt to hedge them against the tail risk of undesirable volatility changes, I don’t know. And I don’t know which kind of hedging our author has in mind.
Creeping
So: Would hedging, as practiced by volatility arbitrageurs, require them to “creep up the moneyness curve”? (As far as I can tell, said “creeping” would involve first trading options far out of the money, and then progressively trading options nearer and nearer the money as part of a hedging strategy.)
Well: Maybe. Assessing this claim in detail would require more information about the hedging strategies of volatility arbitrageurs than I have, but it sounds like the author is just making stuff up at this point.
To drive the VIX up, implied volatility would have to rise, which means that the prices of the options that go into VIX would have to rise, which means someone would have to be buying them. Would volatility arbitrageurs begin by trading out of the money options, and end by buying at the money options to hedge risk?
The only way I can see this making sense is if the arbitrageurs were betting that ultimately realized volatility would be less than that priced into far out of the money options: In such a case they would begin by selling those options. Later, they might buy options nearer the money to protect themselves against a scenario in which volatility rose unexpectedly, and their liabilities were uncapped. So there’s a story for you.
At The Money
Unfortunately, I can’t get past the author’s fixation on at the money options. It’s almost as if he’s thinking of the VXO index (i.e., the original “VIX”), which only considered options at or near the money, as opposed to the modern VIX which considers a broader range of strike prices. In fact, it’s almost as if he not only doesn’t really know what he’s talking about (much like myself) but doesn’t know that he doesn’t know what he’s talking about.
Summary
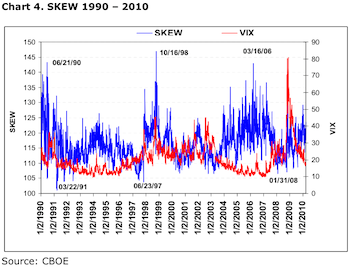
There’s another whole paragraph to go, but I’m calling it here. The author’s whole schtick, once you strip away the smoke, is that a given level of SKEW ought to be associated with a given level of VIX, despite the fact that the two indices measure different bloody things: VIX is the overall “height” of the strike price vs. implied volatility curve, and SKEW is its overall shape. If anything, there seems to be a broad inverse relationship between the two indices:
The author is also fond of assigning single causes to broad market movements (liquidity is suppressing VIX, volatility arbitrageurs will cause VIX and SKEW to converge) and patting himself on the back for his own cleverness (“realities of the options market”, “as many Pros know”, “smarter-than-the-average bear”). He’s definitely a blowhard, and quite possibly a moron. (There is a strong correlation between the BHRD and MRON indices.)
The commenters aren’t much better.
Closing Thoughts and Caveats
This exercise left me with a negative impression of ZH. I realize that they publish a lot of stuff, and that some of it may be better than the rest, but this post strikes me an existence proof of the proposition that there’s a lot of crap there.
On the other hand, maybe I’m just out of my depth, and the author is a genius. But since he doesn’t seem to know the difference between VIX and VXO, I’m not going to waste my time trying to evaluate the merits of any more of his claims. I do hope, however, that this little tour through the land of finance jargon has given you something to think about.